Experiment: A fair coin is flipped until a tail appears.
Find the minimal average number of bits required to encode the outcome of the experiment.
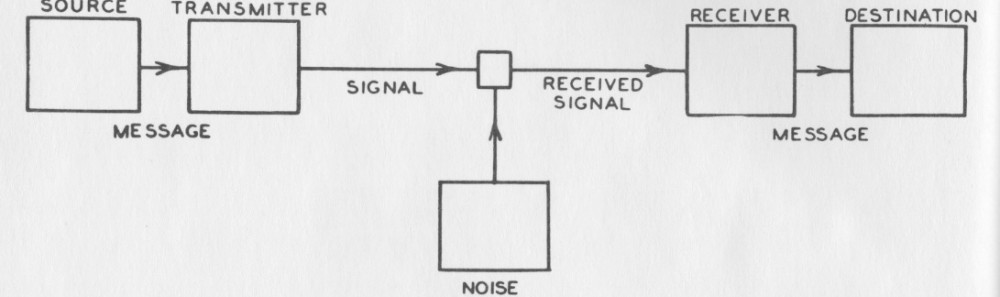
Experiment: A fair coin is flipped until a tail appears.
Find the minimal average number of bits required to encode the outcome of the experiment.
The answer is 0.632843 =
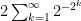
If the first flip is tail, the compressor outputs nothing.
I think he’s referring to the sequence given here ( ): http://oeis.org/A076214 .
): http://oeis.org/A076214 .
Perhaps this interpretation can be added to OEIS.
Ah, I don’t think that is the minimum for a single experiment.
The mapping {1,2}->{0,1},{3,4,5,6}->{00,01,10,11} and so on will give
2 bits