Consider exchangeable random variables 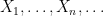 . A couple of facts seem quite intuitive:
. A couple of facts seem quite intuitive:
Statement 1. The “variability” of sample mean 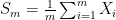 decreases with
decreases with  .
.
Statement 2. Let the average of functions  be defined as
be defined as 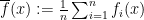 . Then
. Then  is less “variable” than
is less “variable” than 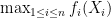 .
.
To make these statements precise, one faces the fundamental question of comparing two random variables 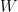 and
and 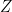 (or more precisely comparing two distributions). One common way we think of ordering random variables is the notion of stochastic dominance:
(or more precisely comparing two distributions). One common way we think of ordering random variables is the notion of stochastic dominance:
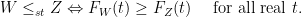
However, this notion really is only a suitable notion when one is concerned with the actual size of the random quantities of interest, while, in our scenario of interest, a more natural order would be that which compares the variability between two random variables (or more precisely, again, the two distributions). It turns out that a very useful notion, used in a variety of fields, is due to Ross (1983): Random variable 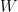 is said to be stochastically less variable than random variable
is said to be stochastically less variable than random variable 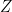 (denoted by
(denoted by 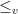 ) when every risk-averse decision maker will choose
) when every risk-averse decision maker will choose 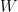 over
over 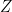 (given they have similar means). More precisely, for random variables
(given they have similar means). More precisely, for random variables 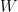 and
and 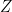 with finite means
with finite means
![\displaystyle W \leq_{v} Z \Leftrightarrow \mathbb{E}[f(X)] \leq \mathbb{E}[f(Y)] \ \ \mbox{ for increasing and convex function } f \in \mathcal{F}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+W+%5Cleq_%7Bv%7D+Z+%5CLeftrightarrow+%5Cmathbb%7BE%7D%5Bf%28X%29%5D+%5Cleq+%5Cmathbb%7BE%7D%5Bf%28Y%29%5D+%5C+%5C+%5Cmbox%7B+for+increasing+and+convex+function+%7D+f+%5Cin+%5Cmathcal%7BF%7D+&bg=ffffff&fg=000000&s=0&c=20201002)
where  is the set of functions for which the above expectations exist.
is the set of functions for which the above expectations exist.
One interesting, but perhaps not entirely obvious, fact is that this notion of ordering 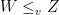 is equivalent to saying that there is a sequence of mean preserving spreads that in the limit transforms the distribution of
is equivalent to saying that there is a sequence of mean preserving spreads that in the limit transforms the distribution of 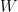 into the distribution of another random variable
into the distribution of another random variable 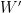 with finite mean such that
with finite mean such that 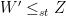 ! Also, using results by Hardy, Littlewood and Polya (1929), the stochastic variability order introduced above can be shown to be equivalent to Lorenz (1905) ordering used in economics to measure income equality.
! Also, using results by Hardy, Littlewood and Polya (1929), the stochastic variability order introduced above can be shown to be equivalent to Lorenz (1905) ordering used in economics to measure income equality.
Now with this, we are ready to formalize our previous statements. The first statement is actually due to Arnold and Villasenor (1986):

Note that when you apply this fact to a sequence of iid random variables with finite mean 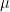 , it strengthens the strong law of large number in that it ensures that the almost sure convergence of the sample mean to the mean value
, it strengthens the strong law of large number in that it ensures that the almost sure convergence of the sample mean to the mean value 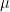 occurs with monotonically decreasing variability (as the sample size grows).
occurs with monotonically decreasing variability (as the sample size grows).
The second statement comes up in proving certain optimality result in sharing parallel servers in fork-join queueing systems (J. 2008) and has a similar flavor:
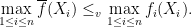
The cleanest way to prove both statements, to the best of my knowledge, is based on the following theorem first proved by Blackwell in 1953 (later strengthened to random elements in separable Banach spaces by Strassen in 1965, hence referred to by some as Strassen’s theorem):
Theorem 1 Let 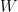 and
and 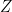 be two random variables with finite means. A necessary and sufficient condition for
be two random variables with finite means. A necessary and sufficient condition for 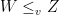 is that there are two random variables
is that there are two random variables 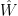 and
and 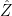 with the same marginals as
with the same marginals as 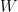 and
and 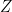 , respectively, such that
, respectively, such that ![{\mathbb{E}[\hat{Z} |\hat{W}] \geq \hat{W}}](https://s0.wp.com/latex.php?latex=%7B%5Cmathbb%7BE%7D%5B%5Chat%7BZ%7D+%7C%5Chat%7BW%7D%5D+%5Cgeq+%5Chat%7BW%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) almost surely.
almost surely.
For instance, to prove the first statement we consider 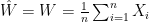 and
and 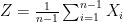 . All that is necessary now is to note that
. All that is necessary now is to note that 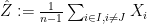 ,
, 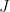 is an independent uniform rv on the set
is an independent uniform rv on the set 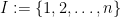 , has the same distribution as random variable
, has the same distribution as random variable 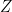 . Furthermore,
. Furthermore,
![\displaystyle \mathbb{E} [ \hat{Z} | W ] = \mathbb{E} [ \frac{1}{n} \sum_{J=1}^{n} (\frac{1}{n-1} \sum_{i\in I, i \neq J} X_i ) | W ] = \mathbb{E} [ \frac{1}{n} \sum_{j=1}^{n} X_j | W ] = W.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cmathbb%7BE%7D+%5B+%5Chat%7BZ%7D+%7C+W+%5D+%3D+%5Cmathbb%7BE%7D+%5B+%5Cfrac%7B1%7D%7Bn%7D+%5Csum_%7BJ%3D1%7D%5E%7Bn%7D+%28%5Cfrac%7B1%7D%7Bn-1%7D+%5Csum_%7Bi%5Cin+I%2C+i+%5Cneq+J%7D+X_i+%29+%7C+W+%5D+%3D+%5Cmathbb%7BE%7D+%5B+%5Cfrac%7B1%7D%7Bn%7D+%5Csum_%7Bj%3D1%7D%5E%7Bn%7D+X_j+%7C+W+%5D+%3D+W.+&bg=ffffff&fg=000000&s=0&c=20201002)
Similarly to prove the second statement, one can construct 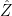 by selecting a random permutation of functions
by selecting a random permutation of functions 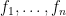 .
.