ORF523: Mirror Prox

Today I’m going to talk about a variant of Mirror Descent invented by Nemirovski in 2004 (see this paper). This new algorithm is called Mirror Prox and it is designed to minimize a smooth convex function $f$ over a compact convex set $\mathcal{X} \subset \mathbb{R}^n$ . We assume that the smoothness is measured in some arbitrary norm $\|\cdot\|$ , precisely we assume that $\forall x, y \in \mathcal{X}, \|\nabla f(x) - \nabla f(y) \|_* \leq \beta \|x - y\|$ .

Let $\Phi : \mathcal{D} \rightarrow \mathbb{R}$ be a mirror map on $\mathcal{X}$ (see this post for a definition) and let $x_1 \in \mathrm{argmin}_{x \in \mathcal{X} \cap \mathcal{D}} \Phi(x)$ . Mirror Prox is described by the following equations:

$\begin{align*} & \nabla \Phi(y_{t+1}') = \nabla \Phi(x_{t}) - \eta \nabla f(x_t), \\ \notag \\ & y_{t+1} \in \mathrm{argmin}_{x \in \mathcal{X} \cap \mathcal{D}} D_{\Phi}(x,y_{t+1}') , \\ \notag \\ & \nabla \Phi(x_{t+1}') = \nabla \Phi(x_{t}) - \eta \nabla f(y_{t+1}), \\ \notag\\ & x_{t+1} \in \mathrm{argmin}_{x \in \mathcal{X} \cap \mathcal{D}} D_{\Phi}(x,x_{t+1}') . \end{align*}$

In words the algorithm first makes a step of Mirror Descent to go from $x_t$ to $y_{t+1}$ , and then it makes a similar step to obtain $x_{t+1}$ , starting again from $x_t$ but this time using the gradient of $f$ evaluated at $y_{t+1}$ (instead of $x_t$ ). The following result justifies the procedure.

Theorem. Let $\Phi$ be a mirror map $\kappa$ -strongly convex on $\mathcal{X} \cap \mathcal{D}$ with respect to $\|\cdot\|$ . Let $R^2 = \sup_{x \in \mathcal{X} \cap \mathcal{D}} \Phi(x) - \Phi(x_1)$ and $f$ be convex and $\beta$ -smooth w.r.t. $\|\cdot\|$ . Then Mirror Prox with $\eta = \frac{\kappa}{\beta}$ satisfies (with $y_1 = x_1$ )

$f\bigg(\frac{1}{t} \sum_{s=1}^t y_s \bigg) - f(x^*) \leq \frac{\beta R^2}{\kappa t} .$

Proof: Let $x \in \mathcal{X} \cap \mathcal{D}$ . We write

$\begin{align*} & f(y_{t+1}) - f(x) \\ & \leq \nabla f(y_{t+1})^{\top} (y_{t+1} - x) \\ & = \nabla f(y_{t+1})^{\top} (x_{t+1} - x) + \nabla f(x_t)^{\top} (y_{t+1} - x_{t+1}) \\ & \qquad + (\nabla f(y_{t+1}) - \nabla f(x_t))^{\top} (y_{t+1} - x_{t+1}) . \end{align*}$

We will now bound separately these three terms. For the first one we have (by definition of the method, first-order optimality condition of the projection, and the definition of the Bregman divergence)

$\begin{align*} & \eta \nabla f(y_{t+1})^{\top} (x_{t+1} - x) \\ & = ( \nabla \Phi(x_t) - \nabla \Phi(x_{t+1}'))^{\top} (x_{t+1} - x) \\ & = ( \nabla \Phi(x_t) - \nabla \Phi(x_{t+1}))^{\top} (x_{t+1} - x) \\ & = D_{\Phi}(x,x_t) - D_{\Phi}(x, x_{t+1}) - D_{\Phi}(x_{t+1}, x_t) . \end{align*}$

For the second term using the same properties than above and the strong-convexity of the mirror map one has

$\begin{align*} & \eta \nabla f(x_t)^{\top} (y_{t+1} - x_{t+1}) \\ & = ( \nabla \Phi(x_t) - \nabla \Phi(y_{t+1}'))^{\top} (y_{t+1} - x_{t+1}) \\ & = ( \nabla \Phi(x_t) - \nabla \Phi(y_{t+1}))^{\top} (y_{t+1} - x_{t+1}) \\ & = D_{\Phi}(x_{t+1},x_t) - D_{\Phi}(x_{t+1}, y_{t+1}) - D_{\Phi}(y_{t+1}, x_t) \\ & \leq D_{\Phi}(x_{t+1},x_t) - \frac{\kappa}{2} \|x_{t+1} - y_{t+1} \|^2 - \frac{\kappa}{2} \|y_{t+1} - x_t\|^2 . \end{align*}$

Finally for the last term, using H\”older’s inequality, $\beta$ -smoothness, and the fact $2 ab \leq a^2 + b^2$ one has

$\begin{align*} & (\nabla f(y_{t+1}) - \nabla f(x_t))^{\top} (y_{t+1} - x_{t+1}) \\ & \leq \|\nabla f(y_{t+1}) - \nabla f(x_t)\|_* \cdot \|y_{t+1} - x_{t+1} \| \\ & \leq \beta \|y_{t+1} - x_t\| \cdot \|y_{t+1} - x_{t+1} \| \\ & \leq \frac{\beta}{2} \|y_{t+1} - x_t\|^2 + \frac{\beta}{2} \|y_{t+1} - x_{t+1} \|^2 . \end{align*}$

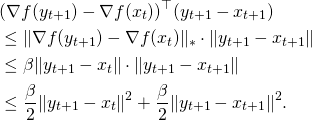
Thus summing up these three terms and using that $\eta = \frac{\kappa}{\beta}$ one gets

$f(y_{t+1}) - f(x) \leq \frac{D_{\Phi}(x,x_t) - D_{\Phi}(x,x_{t+1})}{\eta} ,$

and this inequality is also true for $t=0$ (see the bound for the first term). The proof is then concluded as usual.

$\Box$

Mirror Prox for Saddle Points

Following the generalization of Mirror Descent for Saddle Points (MD-SP, see this post) one can propose a version of Mirror Prox for Saddle Points (MP-SP). In fact the importance of Mirror Prox lies primarily in its application to compute the saddle point of a smooth convex-convave function. Indeed, the key observation is that many non-smooth convex functions admit a smooth saddle-point representation (see examples below). With such a representation one can then use MP-SP to obtain a rate of convergence of order $1/t$ , despite the fact that the original function is non-smooth! Recall that we proved that for non-smooth convex functions the optimal black-box rate is of order $1/\sqrt{t}$ . However MP-SP is not a black-box method in the sense that it makes use of the structure of the function (by representing it as a saddle-point). Nonetheless MP-SP still enjoys the nice time-complexity property of black-box methods since it is a first-order method. It is a win-win situation!

Let us now describe more precisely MP-SP. Let $\mathcal{X} \subset \mathbb{R}^n$ be a compact and convex set endowed with some norm $\|\cdot\|_{\mathcal{X}}$ and a mirror map $\Phi_{\mathcal{X}}$ (defined on $\mathcal{D_{\mathcal{X}}}$ ), and let $\mathcal{Y} \subset \mathbb{R}^m$ be a compact and convex set endowed with some norm $\|\cdot\|_{\mathcal{Y}}$ and a mirror map $\Phi_{\mathcal{Y}}$ (defined on $\mathcal{D_{\mathcal{Y}}}$ ). Let $\phi : \cX \times \cY \rightarrow \mathbb{R}$ be a continuously differentiable function such that $\phi(\cdot, y)$ is convex and $\phi(x, \cdot)$ is concave. We assume that $\phi$ is $(\beta_{11}, \beta_{12}, \beta_{22}, \beta_{21})$ -smooth in the sense that:

$\begin{align*} & \|\nabla_x \phi(x,y) - \nabla_x \phi(x',y) \|_{\mathcal{X},*} \leq \beta_{11} \|x-x'\|_{\mathcal{X}} , \\ & \|\nabla_x \phi(x,y) - \nabla_x \phi(x,y') \|_{\mathcal{X},*} \leq \beta_{12} \|y-y'\|_{\mathcal{Y}} , \\ & \|\nabla_y \phi(x,y) - \nabla_y \phi(x,y') \|_{\mathcal{Y},*} \leq \beta_{22} \|y-y'\|_{\mathcal{Y}} , \\ & \|\nabla_y \phi(x,y) - \nabla_y \phi(x',y) \|_{\mathcal{Y},*} \leq \beta_{21} \|x-x'\|_{\mathcal{X}} , \\ \end{align*}$

We consider the mirror map $\Phi((x,y)) = \Phi_{\mathcal{X}}(x) + \Phi_{\mathcal{Y}}(y)$ on $\mathcal{Z} = \mathcal{X} \times \mathcal{Y}$ (defined on $\mathcal{D} = \mathcal{D_{\mathcal{X}}} \times \mathcal{D_{\mathcal{Y}}}$ ). Let $z_1 \in \mathrm{argmin}_{z \in \mathcal{Z} \cap \mathcal{D}} \Phi(z)$ . Then for $t \geq 1$ , let $z_t=(x_t, y_t)$ and $w_t=(u_t,v_t)$ be defined by the following equations (with $w_1=z_1$ ):

$\begin{align*} & \nabla \Phi(w_{t+1}') = \nabla \Phi(z_{t}) - \eta (\nabla_x \phi(x_t, y_t), - \nabla_y \phi(x_t, y_t)), \\ \notag \\ & w_{t+1} \in \mathrm{argmin}_{z \in \mathcal{Z} \cap \mathcal{D}} D_{\Phi}(z,w_{t+1}') , \\ \notag \\ & \nabla \Phi(z_{t+1}') = \nabla \Phi(z_{t}) - \eta (\nabla_x \phi(u_t, v_t), - \nabla_y \phi(u_t, v_t)), \\ \notag\\ & z_{t+1} \in \mathrm{argmin}_{z \in \mathcal{Z} \cap \mathcal{D}} D_{\Phi}(z,z_{t+1}') . \end{align*}$

Theorem. Assume that $\Phi_{\mathcal{X}}$ is $1$ -strongly convex on $\mathcal{X} \cap \mathcal{D}_{\mathcal{X}}$ with respect to $\|\cdot\|_{\mathcal{X}}$ and let $R^2_{\mathcal{X}} = \sup_{x \in \mathcal{X} \cap \mathcal{D}} \Phi_{\mathcal{X}}(x) - \inf_{x \in \mathcal{X} \cap \mathcal{D}} \Phi_{\mathcal{X}}(x)$ (with similar definition for $\Phi_{\mathcal{Y}}$ ). Let $\beta = \max(\beta_{11}, \beta_{12}, \beta_{22}, \beta_{21})$ . Then SP Mirror Descent with $\eta = \frac{1}{2 \beta}$ satisfies

$\max_{y \in \mathcal{Y}} \phi\left( \frac1{t} \sum_{s=1}^t u_s,y \right) - \min_{x \in \mathcal{X}} \phi\left(x, \frac1{t} \sum_{s=1}^t v_s \right) \leq \frac{2 \beta (R^2_{\mathcal{X}} + R^2_{\mathcal{X}})}{t}.$

Proof: First we endow $\mathcal{Z}$ with the norm defined by

$\|z\|_{\mathcal{Z}} = \sqrt{\|x\|_{\mathcal{X}}^2 + \|y\|_{\mathcal{Y}}^2} .$

It is immediate that $\Phi$ is $1$ -strongly convex with respect to $\|\cdot\|_{\mathcal{Z}}$ on $\mathcal{Z} \cap \mathcal{D}$ . Furthermore one can easily check that

$\|z\|_{\mathcal{Z},*} = \sqrt{\|x\|_{\mathcal{X},*}^2 + \|y\|_{\mathcal{Y},*}^2} ,$

and thus the vector fields $(\nabla_x \phi(x, y), - \nabla_y \phi(x,y))$ used in MP-SP satisfy:

$\|(\nabla_x \phi(x, y), - \nabla_y \phi(x,y)) - (\nabla_x \phi(x', y'), - \nabla_y \phi(x',y'))\|_{\mathcal{Z},*}^2 \leq 4 \beta^2 \|(x,y) - (x',y') \|_{\mathcal{Z}}^2 .$

It suffices now to use the exact same proof than for the standard Mirror Prox starting with:

$\begin{eqnarray*} \phi\left( \frac1{t} \sum_{s=1}^t x_s,y \right) - \phi\left(x, \frac1{t} \sum_{s=1}^t y_s \right) & \leq & \frac{1}{t} \sum_{s=1}^t \bigg( \phi\left(x_s,y \right) - \phi\left(x, y_s \right) \bigg) \\ & \leq & \frac{1}{t} \sum_{s=1}^t g_s^{\top} (z_s - z) . \end{eqnarray*}$

$\Box$

Smooth saddle-point representation of non-smooth functions

Assume that the function $f$ to be optimized is of the form:

$f(x) = \max_{1 \leq i \leq m} f_{i} (x) ,$

where the functions $f_i(x)$ are convex, $\beta$ -smooth and $L$ -Lipschitz in some norm $\|\cdot\|$ . Minimizing $f$ over $\mathcal{X}$ is equivalent to finding a saddle point over $\mathcal{X} \times \Delta_{m}$ since one has:

$f(x) = \max_{y \in \Delta_{m}} y^{\top} (f_1(x), \hdots, f_{m}(x)) .$

Thus we are looking for the saddle point of $\phi(x,y) = y^{\top} (f_1(x), \hdots, f_{m}(x))$ which is convex in $x$ , and concave (in fact linear!) in $y$ . Furthermore $\phi$ is smooth and it is an easy exercise to verify that in this case one has $\beta_{22} = 0$ , $\beta_{21} = L$ , $\beta_{11} = \beta$ , and $\beta_{12} = L$ . Thus a rate of convergence (to the minimizer of $f$ ) of order $(\beta + L) (R^2_{\mathcal{X}} + \log(\ell)) /t$ can be obtained by applying MP-SP with appropriate mirror maps (in particular the update in the $y$ -space has to be done with the negative entropy). Note that is rate is particularly striking since the oracle lower bound of $1/\sqrt{t}$ was proved precisely for this type of function! Here we are able to get around this lower bound by making use of the structure of the function. Remark also that if you think about what this algorithm is doing to optimize the function $f$ you get a very very elegant procedure for which it is highly non-trivial a priori to prove something about its rate of convergence.

Finally note that if $\beta$ and $L$ are of different order of magnitudes one can obtain a better result by considering the mirror map $\Phi((x,y)) = a \Phi_{\mathcal{X}}(x) + b \Phi_{\mathcal{Y}}(y)$ and optimizing over the values of $a$ and $b$ .

Another interesting example arises when $\phi(x,y) = x^{\top} A y$ with $A \in \mathbb{R}^{n \times m}$ , $\mathcal{X} = \Delta_n$ and $\mathcal{Y} = \Delta_m$ . With the $\ell_1$ -norm on both spaces it is easy to see that $\beta_{12} = \beta_{21} = \| A \|_{\mathrm{max}}$ (the entrywise max norm), and of course $\beta_{11} = \beta_{22} = 0$ . Thus we obtain here a convergence rate of order $\| A \|_{\mathrm{max}} (\log(n) + \log(m)) / t$ . Again if $n$ and $m$ are of different order of magnitudes one can improve the result to obtain a rate of order $\| A \|_{\mathrm{max}} \sqrt{\log(n) \log(m)} / t$ by considering the mirror map $\Phi((x,y)) = a \Phi_{\mathcal{X}}(x) + b \Phi_{\mathcal{Y}}(y)$ and optimizing over the values of $a$ and $b$ .

Many more interesting examples can be derived and we refer the reader to the original paper of Nemirovski as well as this book chapter by Juditsky and Nemirovski.

2 Responses to "ORF523: Mirror Prox"

By Alexander Gasnikov (MIPT) January 9, 2014 - 3:01 pm

The same results can be obtained by the Nesterov’s smoothing technique
http://luthuli.cs.uiuc.edu/~daf/courses/Optimization/MRFpapers/nesterov05.pdf
- By Sebastien Bubeck March 15, 2014 - 11:51 am
  
  Yes I agree! However it is not clear to me under what circumstances Nesterov’s smoothing should be preferred to Mirror Prox. Do you have any intuition about this?

Nov	APR	Nov
	25
2016	2021	2022

ORF523: Mirror Prox

2 Responses to "ORF523: Mirror Prox"

By Alexander Gasnikov (MIPT) January 9, 2014 - 3:01 pm

By Sebastien Bubeck March 15, 2014 - 11:51 am

Leave a reply

Archives

Categories

Recent Posts

Subscribe to Blog via Email

Meta

Blogroll